とにかくまずは動かして感じを掴んでみましょう。

正しくインストールされていれば CoqIDE が普通のアプリケーションとして起動できるはずです。

Ubuntuの場合

起動したところ

試しに次のスクリプト

Require Import ssreflect.

Section Tutorial.

  Variable A B C : Prop.

  Lemma HilbertS : (A -> B -> C) -> (A -> B) -> A -> C.
  Proof.
    move => g.
    move => f.
    move => x.
    apply g.
    apply x.
    apply f.
    apply x.
  Qed.

End Tutorial.

をコピペして、左上の下向き矢印アイコンをポチポチ押してみてください。

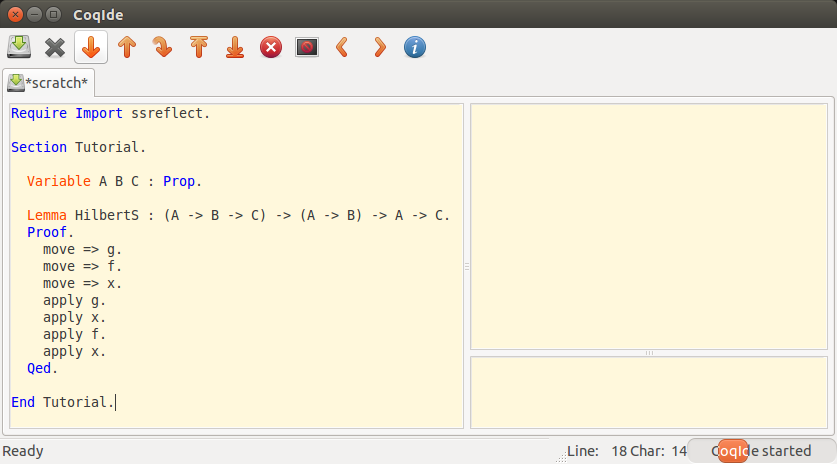
入力したところ

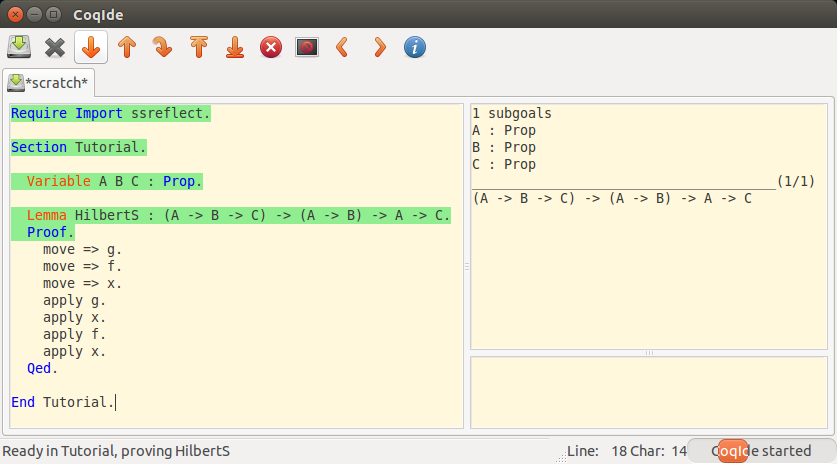
ポチポチ

緑の範囲選択が Qed. に到達して右下の窓に HilbertS is defined と表示されたら証明完了です。

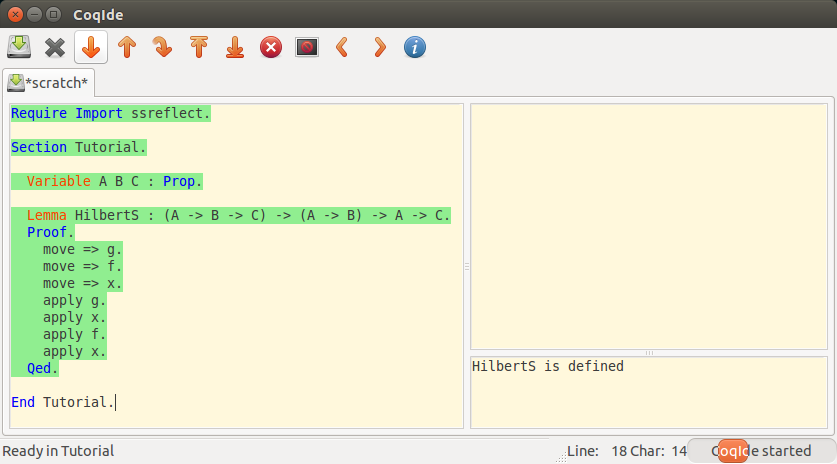
証明完了!

解説

まずは全体の説明をします。

Coq は大文字と小文字を区別します。日本語等の Unicode 文字も扱えるようです。
改行やインデントは空白と同じ扱いです。読みやすいように好みで整形してください。
(* と *) に囲まれた範囲はコメントとして無視されます。コメントはネスト可能です。
Coq の文の最初の単語は Command か tactic です。 Command (Section, Lemma, ...) は英大文字から、 tactic (move, apply, ...) は英小文字から始まります。 tactic は証明環境 (Proof. と Qed. の間) でのみ使えます。
Coq の文はピリオド . で終わります。つけ忘れに注意しましょう。

次に先程入力したスクリプト

Require Import ssreflect.

Section Tutorial.

  Variable A B C : Prop.

  Lemma HilbertS : (A -> B -> C) -> (A -> B) -> A -> C.
  Proof.
    move => g.
    move => f.
    move => x.
    apply g.
    apply x.
    apply f.
    apply x.
  Qed.

End Tutorial.

の各文を見て行きましょう。

Require Import ssreflect.

Ssreflect拡張を読み込みます。 C 言語の #include <stdio.h> みたいなものだと思って冒頭に書いておきましょう。
Section Tutorial.

セクションを開始します。 Tutorial の部分には好きな名前がつけられます。セクション内で宣言された変数は同一セクション内からのみ参照できます。セクションはネスト可能です。
Variable A B C : Prop.

変数宣言です。「以下、この章では A, B, C は命題とする。」といったところです。
Lemma HilbertS : (A -> B -> C) -> (A -> B) -> A -> C.

補題です。 HilbertS はこの補題につけられる名前です。 -> はとりあえず「ならば」と読めばよく、右結合なのであえて括弧をつければ (A -> (B -> C)) -> ((A -> B) -> (A -> C)) となります。これは Hilbert System の公理の一つです。
Proof.

ここから Qed. までが証明環境です。 tactic を使って証明を操作していきます。証明の進捗状況が右上の窓に表示されるので上下の矢印アイコンで操作しながら見て行きましょう。

証明開始
```
1 subgoals
A : Prop
B : Prop
C : Prop
______________________________________(1/1)
(A -> B -> C) -> (A -> B) -> A -> C
```
最初の行は subgoal が１つであることを示します。罫線の上は context と呼ばれ、証明の中で使える仮定です。罫線の下にあるのが subgoal で、これを context から導出できれば証明完了です。今は補題そのものが subgoal になっています。
move => g. move => f. move => x.

subgoal が (A -> B -> C) -> (A -> B) -> A -> C なので、 A -> B -> C を仮定して (A -> B) -> A -> C を示せばよいでしょう。それを実現するのが move tactic で、 move => g. により subgoal の仮定 A -> B -> C を context に持ち上げ g と名付けます。あとの２つも同様です。３文に分けて行いましたが move => g f x. とまとめて行うこともできます。

この時点で context と subgoal は以下のようになっているはずです。
```
1 subgoals
A : Prop
B : Prop
C : Prop
g : A -> B -> C
f : A -> B
x : A
______________________________________(1/1)
C
```
apply g.

subgoal C を示したいわけですが context に g : A -> B -> C があるので、 A と B を示せばよいでしょう。それを実現するのが apply tactic で、 apply g. により subgoal が A と B の２つに置き換えられます。
apply x.

subgoal が２つに増えましたが上から順に示せばよいです。１つめの subgoal は A ですが context に x : A があるので、 apply x. とすることでこの subgoal は導出されます。導出された subgoal は見えなくなります。
apply f.

残った subgoal は B ですが context に f : A -> B があるので、 apply f. とすることで A に置き換わります。
apply x.

この A も apply x. とすれば導出されます。
Qed.

すべての subgoal が導出されたので Qed. として証明完了です。
End Tutorial.

セクションを閉じます。セクション Tutorial の中で宣言された A, B, C にはアクセスできなくなります。

背景

上でみたような命題の証明の背景にあるのはカリー＝ハワード同型対応と呼ばれる証明論と型システムの間の対応です。ここでは型システムとして型付きラムダ計算を考えます。

今後の解説に必要な範囲で簡単に説明しておきます。文法は Coq のものと揃えておきます。

a : A と書いたら「a は型 A を持つ」と読みます。型付きラムダ計算は２つの公理からなります。

関数適用

a : A かつ f : A -> B ならば f a : B が成り立つ。
関数抽象

仮定 x : A のもと y : B ならば、仮定 x : A なしに fun x : A => y : A -> B が成り立つ。但し、一般に y は x に依存する。

カリー＝ハワード同型対応にしたがって型付きラムダ計算と証明論を比較してみます。参考に集合論も加えておきます。

型付きラムダ計算

`a : A`	`a` は型 `A` を持つ。
`A -> B`	`A` から `B` への関数の型。
`f a`	`f : A -> B` に `a : A` を適用。型は `B`。
`fun x : A => y`	`x : A` に `y : B` を対応させる関数。型は `A -> B`。

証明論

`a : A`	`a` は命題 `A` の証明。
`A -> B`	命題「`A` ならば `B`」。
`f a`	`A -> B` の証明 `f` と `A` の証明 `a` から得られる `B` の証明。
`fun x : A => y`	`x` を `A` の証明と仮定して `B` の証明 `y` を与える。これは、`A -> B` の証明となる。

集合論

\(a \in A\)	\(a\) は集合 \(A\) の元。
\(\mathrm{Map}(A, B)\)	\(A\) から \(B\) への写像の集合。
\(f(a)\)	\(f \in \mathrm{Map}(A, B)\) に \(a \in A\) を適用。これは \(B\) の元。
\(A \ni x \mapsto y\)	\(A\) の元 \(x\) に \(B\) の元 \(y\) を対応させる写像。これは \(\mathrm{Map}(A, B)\) の元。

このあたりを踏まえて HilbertS の証明を見てみましょう。

HilbertS の証明が完了している段階で Escape (もしくは Navigation から Show Query Pane) を押して、

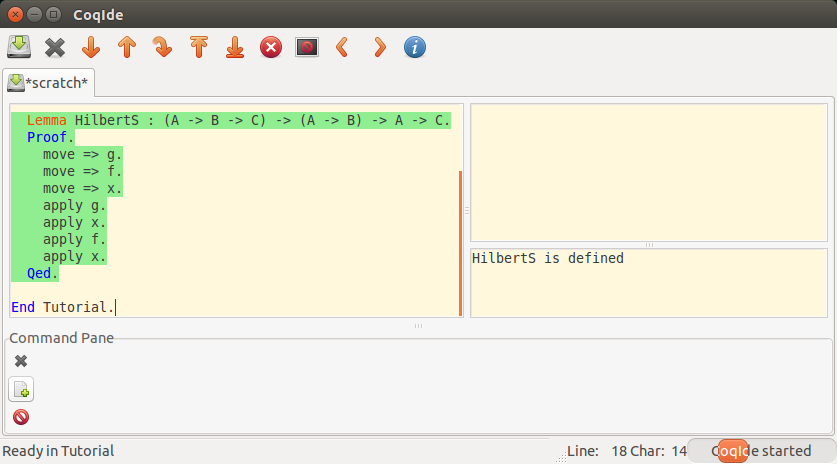
新規作成っぽいボタンを押して、 Print と HilbertS と入力して Ok を押してみてください。

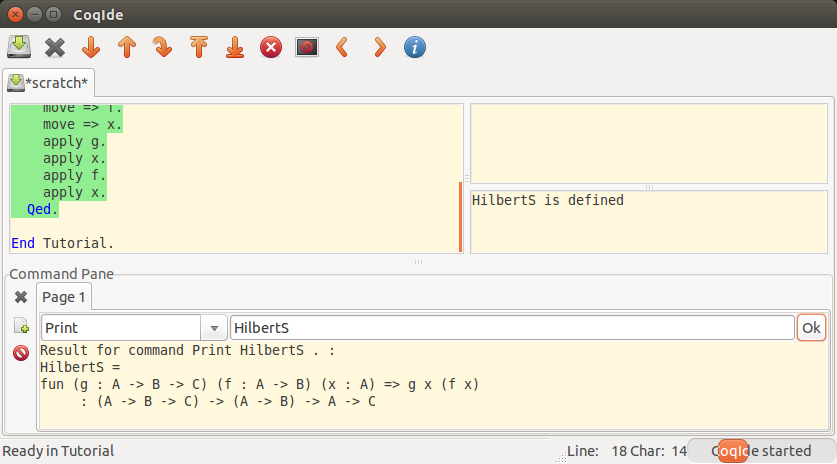
そこに表示されている

fun (g : A -> B -> C) (f : A -> B) (x : A) => g x (f x)

がさっき書いた証明に対応するプログラム (ラムダ項) です。これは

fun g : A -> B -> C => fun f : A -> B => fun x : A => g x (f x)

の略記です。関数適用は左結合なので g x (f x) は括弧をつけると (g x) (f x) となります。

型付きラムダ計算の公理から、上の式の型を確認してみましょう。

g : A -> B -> C, f : A -> B, x : A を仮定します。
関数適用により f x : B が得られます。
関数適用により g x : B -> C が得られます。
関数適用により g x (f x) : C が得られます。
関数抽象により仮定 x : A を外して fun x : A => g x (f x) : A -> C が得られます。
関数抽象により仮定 f : A -> B を外して fun f : A -> B => fun x : A => g x (f x) : (A -> B) -> A -> C が得られます。
関数抽象により仮定 g : A -> B -> C を外して fun g : A -> B -> C => fun f : A -> B => fun x : A => g x (f x) : (A -> B -> C) -> (A -> B) -> A -> C が得られます

以上の議論から

fun (g : A -> B -> C) (f : A -> B) (x : A) => g x (f x)

は型

(A -> B -> C) -> (A -> B) -> A -> C

を持つことが分かりました。カリー＝ハワード同型対応より、命題 (A -> B -> C) -> (A -> B) -> A -> C の証明が得られました。

Coq で書いた証明は今行った議論を逆にたどりながら構成しているのがわかるでしょうか。

Top Next

動かしてみる

解説

背景